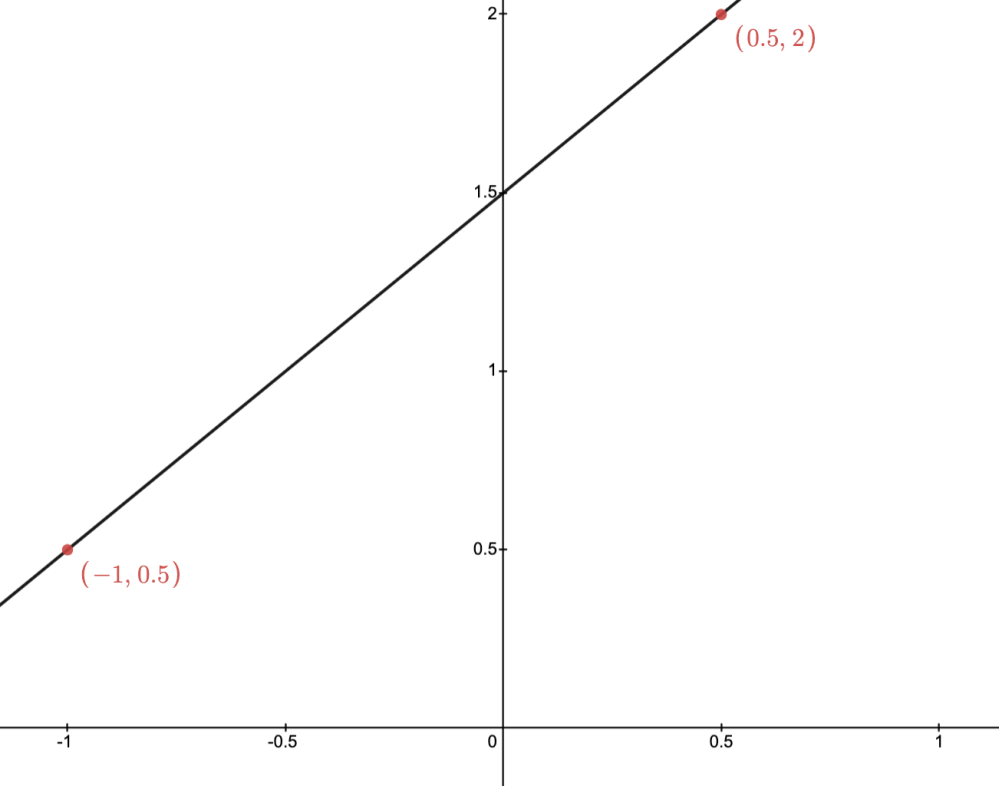These are notes used for lecturing ECSE 507 during the Winter 2024 semester.
Please note that these notes constantly evolve and beware of typos/errors.
These notes are heavily influenced by Boyd and Vandenberghe’s text Convex Optimization.
I appreciate being informed about typos/errors in these notes.
Click each subject to unfold.
Introduction
General Problem
Interested in solving and studying minimization problems subject to constraints:
-
are problem parameters;
-
is the objective function and
usually interpreted as cost for choosing
;
-
is a constraint set often described “geometrically”.
Example 1. Design Problem Interpretation
Let=scalar-valued design variables
(e.g., dimensions of manufactured object, yaw and pitch of jet).= penalty for choosing design
(e.g., cost in material, energy, time, deviation from desired path).= design specifications
(i.e., allowable/possible values for).
E.g.,specifies minimum and maximum design values.
Problems With Structure
General optimization problems can be numerically inefficient to solve or analytically difficult, unlessIdentifying nice structure/properties of problem
Examples of nice structure:
E.g.,
If
Linear Programming
Simplest case:Notation: if
means
for
.
Linear program: given
Positives of linear programming:
- Conceptually simple: relies heavily on linear algebra
- There are classical numerical methods which are often very efficient.
- If
is local minimizer of
on
, then it is automatically a global minimizer on
.
- Can sometimes approximate smooth problems linearly; however, usually can only give “local” results.
(E.g.,for
.)
Shortcomings of linear programming:
- Many applied problems are not linear.
- Many problems may not even be (suitably) approximated by linear programs.
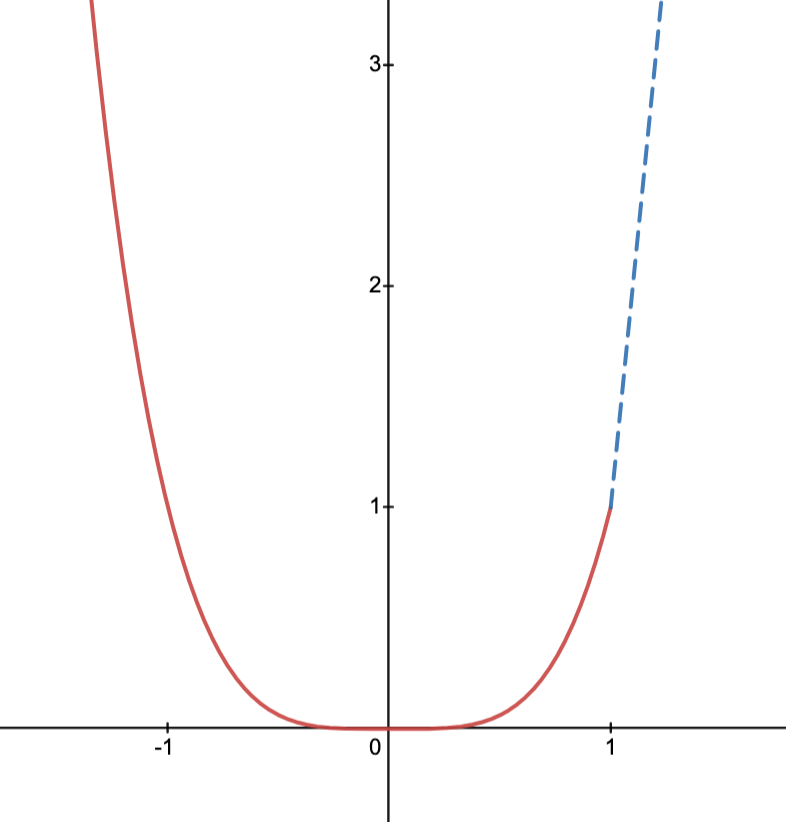
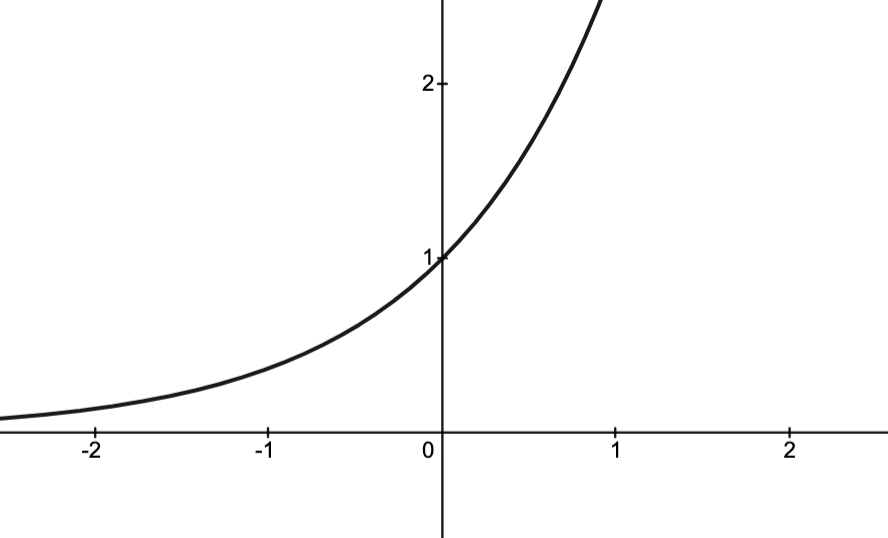
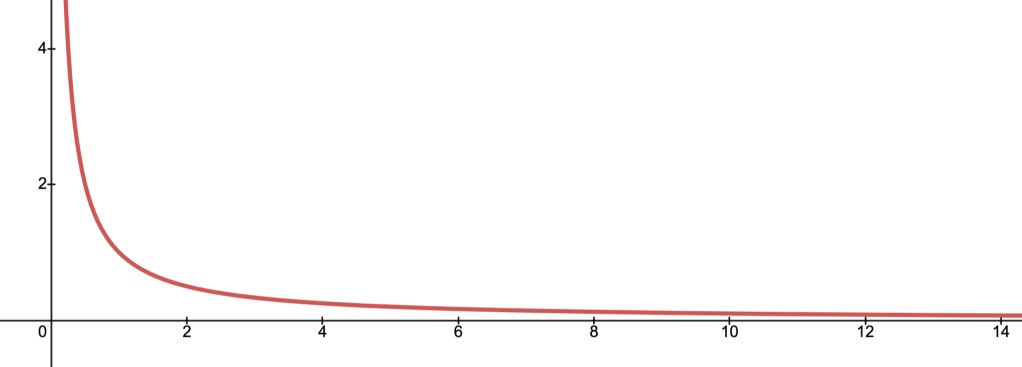
E.g., the “barrier”
is better approximated by the a “logarithmic barrier” of the formthan any linear function.
Convex Optimization
Convex optimization problem:This is the main focus of the course.
Positives of Convex Optimization:
- Relatively conceptually simple.
- Still often have efficient, albeit more sophisticated, numerical methods.
- Many applied problems may be recast as or approximated by convex optimization problems.
- If
is local minimizer of
on
, then it is automatically a global minimizer on
.
Shortcomings of Convex Optimization:
Example (Least Squares)
A standard and ubiquitous kind of convex optimization problem is the least squares problem.This problem takes the form:
is some norm
a matrix
a fixed vector
is the (convex) objective function
are convex.
Optimal Control
Let-
be functions
.
-
is the time derivative of
.
-
are assumed to be given;
-
we think of
as being the state of some system at time
;
- we think of
as an input we are allowed to choose to dictate the evolution
of
; i.e.,
“controls” the system;
- When
, the system experiences “feedback.”
-
the goal: choose control law
so that
is as “desirable” as possible.
Example: Optimal Control Problems
Optimal control problem: choose the “best” controlTypically “best” and “desirable” are determined by size/cost of
Rough Outline of Course
- Part 1: Basics of Convexity and Convex Optimization Problems.
- Part 2: Applications of Convex Optimization Problems.
- Part 3: Algorithms for Solving Convex Optimization Problems.
- Part 4: Topics in Optimal Control.
Convex Geometry
Convex Sets
Convex set: a subset
for all and
, there holds
.
Examples: some standard convex sets.
- Closed or open polytopes in
.
E.g., the interior of a tetrahedron. - Euclidean balls, ellipsoids.
- Linear subspaces and affine spaces (e.g., lines, planes).
- Given a norm
on
, the
-ball
with centerand radius
is a convex set.
Recall: a norm satisfies-
for all vectors
;
-
for all vectors
and scalars
;
-
iff
.
-
Affine Subsets
Affine subset: A subset
For all and
, there holds
.
N.B.: An affine subset is just a translated linear subspace:
“a linear space that’s forgotten its origin”.
Example 1.
LetThen any translation or rotation of
Example 2.
If(
Cones
Cone: A subset
For all and
, there holds
.
Proposition.
Proof.
Step 1. ( )
)
Suppose Want to show:
Step 2.
Being conic impliesStep 3.
Being convex impliesStep 4. ( )
)
Suppose Want to show:
Step 5.
Step 6.
Convexity follows from takingIndeed:
Examples.
- Hyperplanes
with normal
,
halfspaces,
nonnegative orthantsare all convex cones.
(Here,if
for
.)
-
Given a norm
on
, the
-norm cone is
which is a convex cone in,
.
- See “positive semidefinite cone” below.
Polyhedra
Polyhedron: Any subset
Thus,
N.B.: Introducing equality constraints can be used to reduce dimension.
Positive Semidefiniteness
Symmetric matrix:
a matrix
Positive semidefinite matrix:
Equivalently,
If
If
Set of symmetric positive semidefinite matrices:
Positive definite matrix:
Equivalently,
If
If
Set of symmetric positive definite matrices:
Example 1
LetSince
To see
with
Example 2.
LetSince
To see
Example 3.
LetOne can conclude
To see it directly, compute
Example 4.
LetWe can conclude
Positive Semidefinite Cone
Proposition 1.Proof.
Step 1.
 is a vector space:
is a vector space:
if
.
Step 2.
 :
:
since
Counting the number of bold entries shows
Step 3.
 is a convex cone:
is a convex cone:
For
,
By the proposition in Convex Geometry.Cones, we conclude the desired result.
Proposition 2.
and
.
Proof.
Step 1.
Let
recalling that
Step 2. (Case  )
)
First compute
for all
iff
.
Can thus conclude (in case
for all
iff
.
Step 3. (Case  )
)
Completing the square gives
for all
iff
and
.
N.B.: strictly speaking,
Step 4.
Putting Steps 2. and 3. together, we conclude:
and
.
Separating Hyperplanes
LetSeparating hyperplane: a hyperplane given by
Thus,
Separating Hyperplane Theorem. If
Supporting Hyperplanes
Let
.
Equivalently,
(Here:
Hulls
LetConvex hull:
the set
.
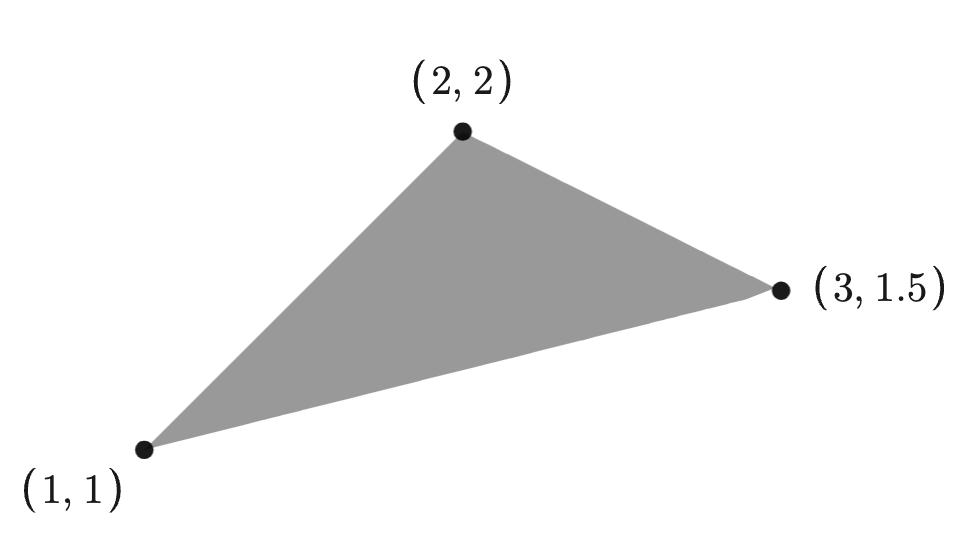
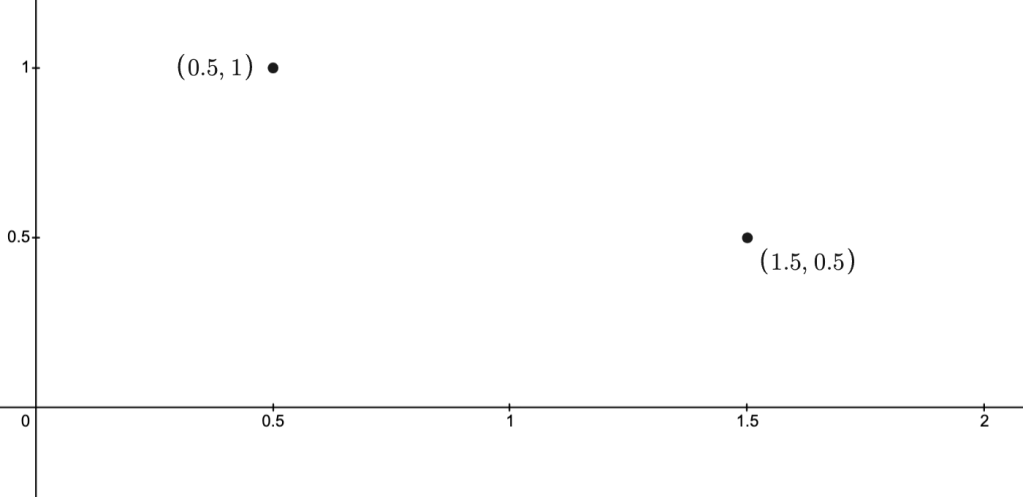
Example: The images below depict a set of three points and its convex hull.
Affine hull:
the set
.
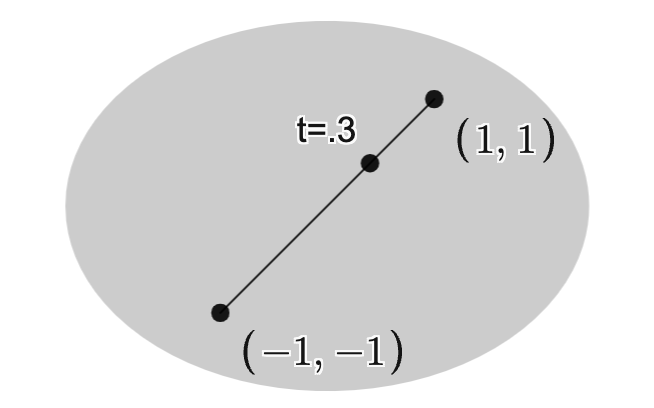
Example: The images below depict two points and their affine hull.
Conic hull:
The set
.
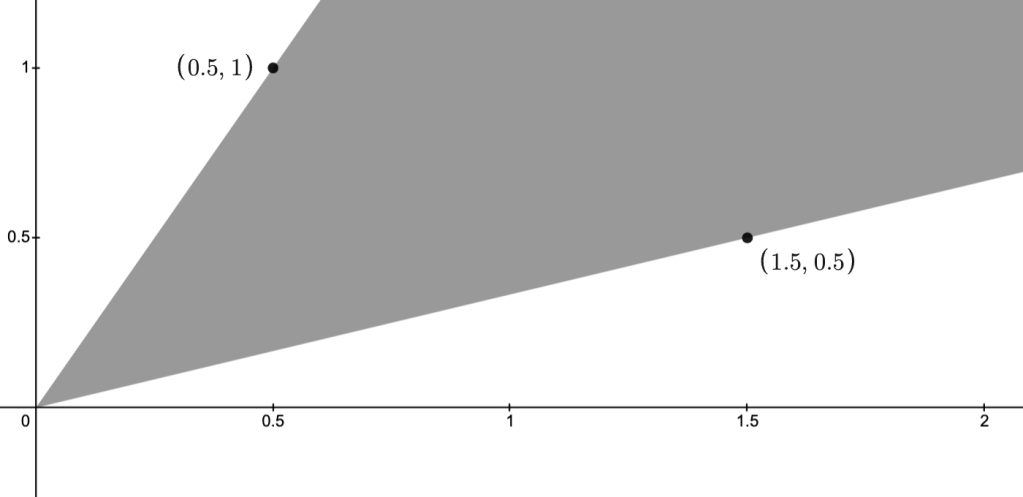
Example: The images below depict two points
Details
To see that the conic hull really is the shaded region, note that, by takingThus, it contains all line segments connecting any two points on the nonnegative rays
N.B.:
- Conic hulls are convex cones.
-
Taking the “___ hull” of
does indeed result in a “___” set.
-
The “___ hull” is a construction of the smallest “___” subset containing
.
Generalized Inequalities
Proper cone: a convex cone-
is closed (i.e.,
contains its boundary)
-
has nonempty interior
-
.
.
.
Examples
-
(CO Example 2.14)
If, then
is the standard componentwise vector inequality:
N.B.:.
is the standard inequality on
.
-
(CO Example 2.15)
If, then
.
-
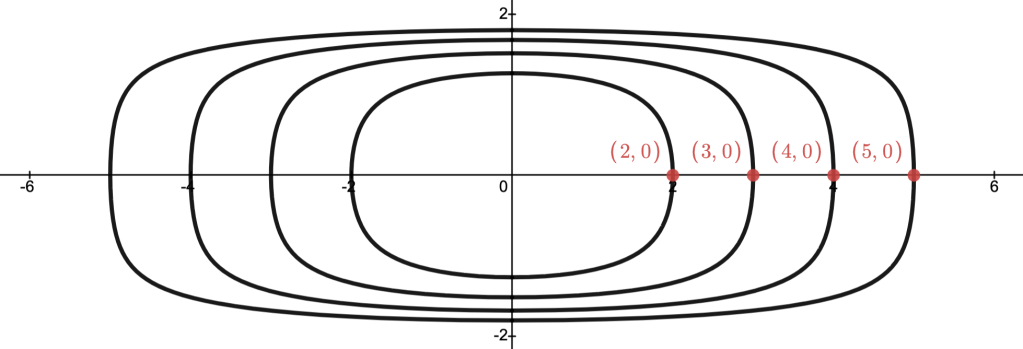
Let
Then.
is a proper cone.
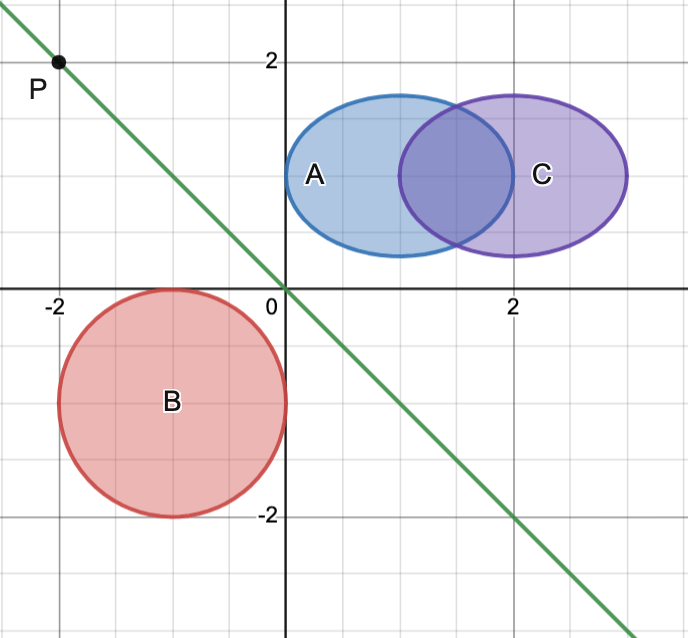
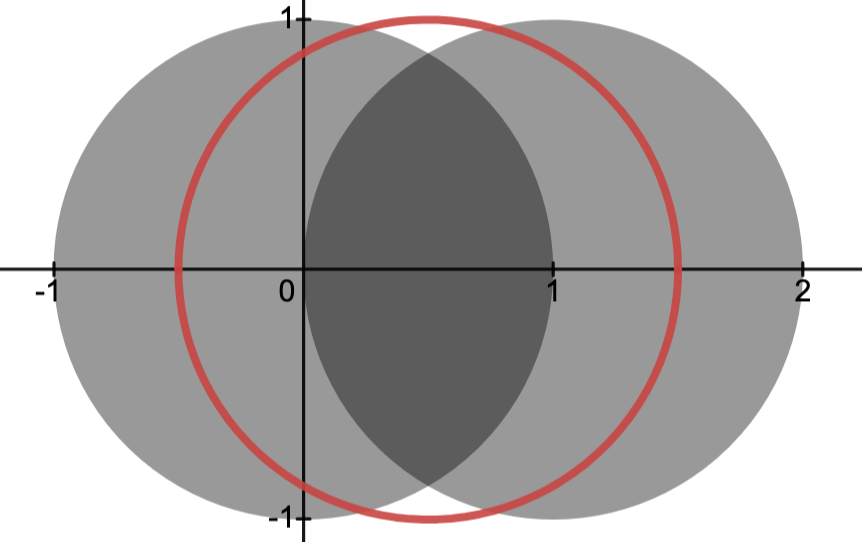
In the image below:-
is the cone with vertex
.
-
The cone with vertex
depicts those
with
.
-
The cone with vertex
depicts those
with
.
, and so
, as indicated in the image.
Moreover,and
are not comparable.
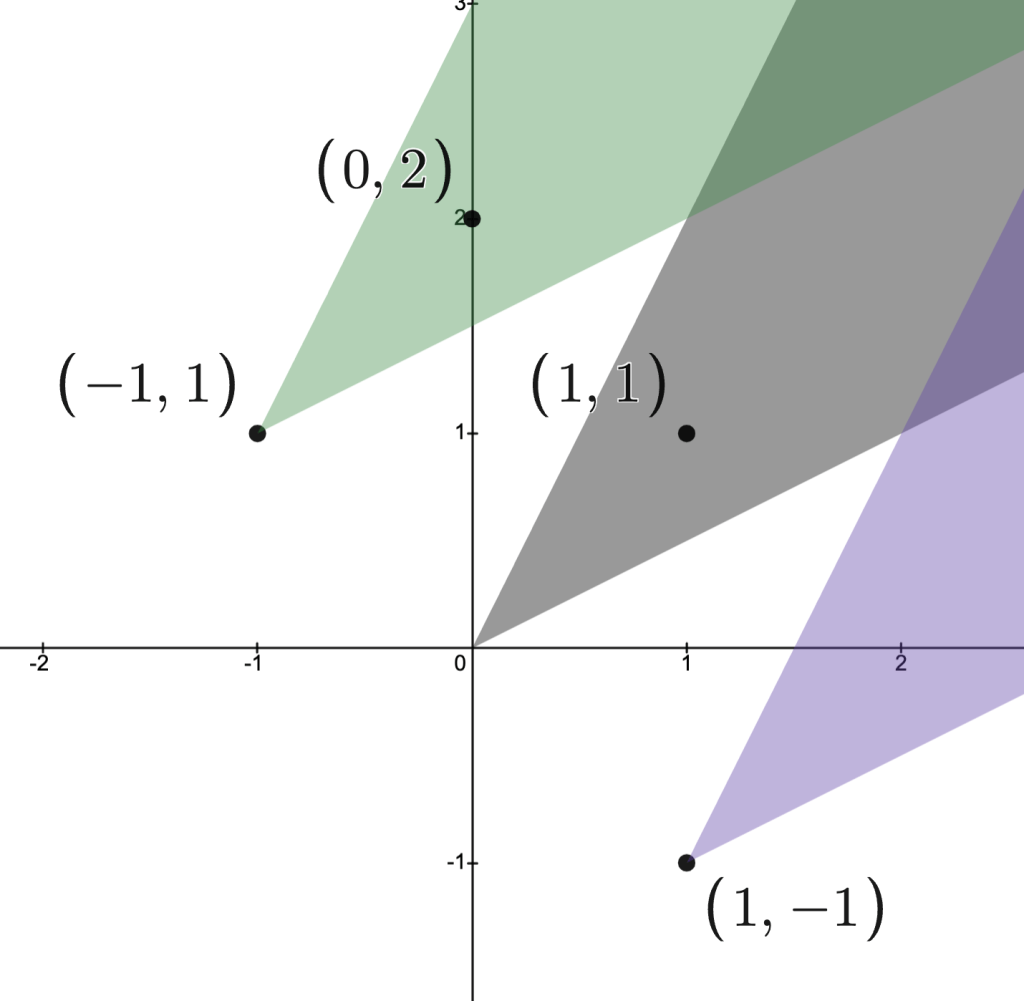
-
Convex Function Theory
Conventions and Notations
-
Writing
always means a partial function with domain
possibly smaller than
.
“Function” will mean “partial function.” - If
, we may work with the extension
given by
It is common to implicitly assumehas been extended and to write
for the partial function
and its extension
.
-
Given a set
, its indicator function is
- We write
Convex Functions
LetStrict convexity:
for all
.
Remarks.
- It is instructive to compare convexity/concavity with linearity and view the former as weak versions of linearity.
- It is common to extend the definition of convexity to extended functions, i.e., those of the form
.
For example, the indicator functionis convex in this sense.
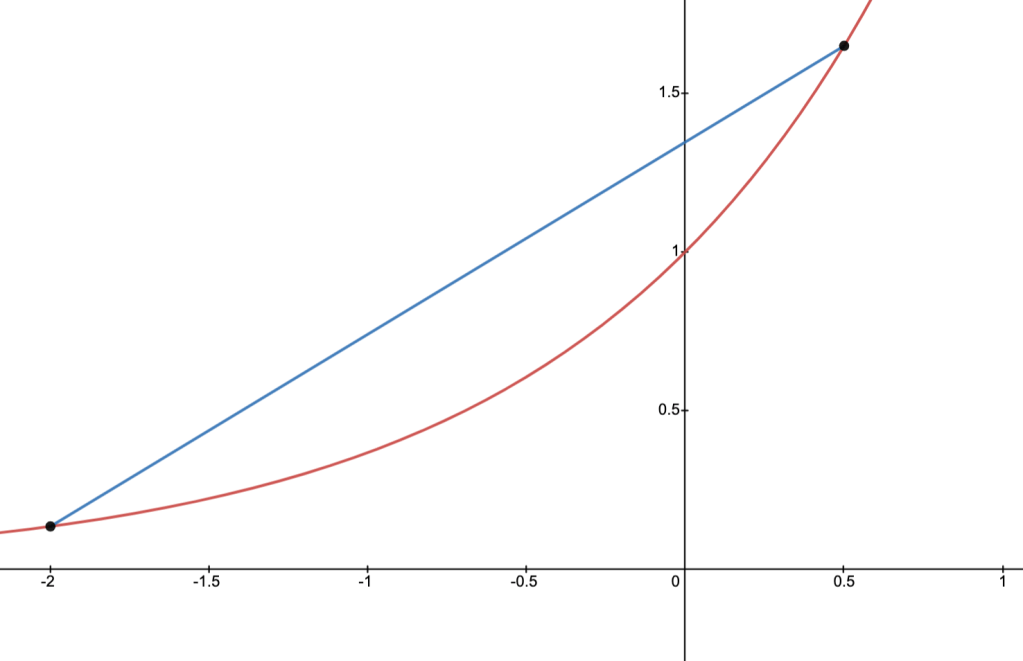
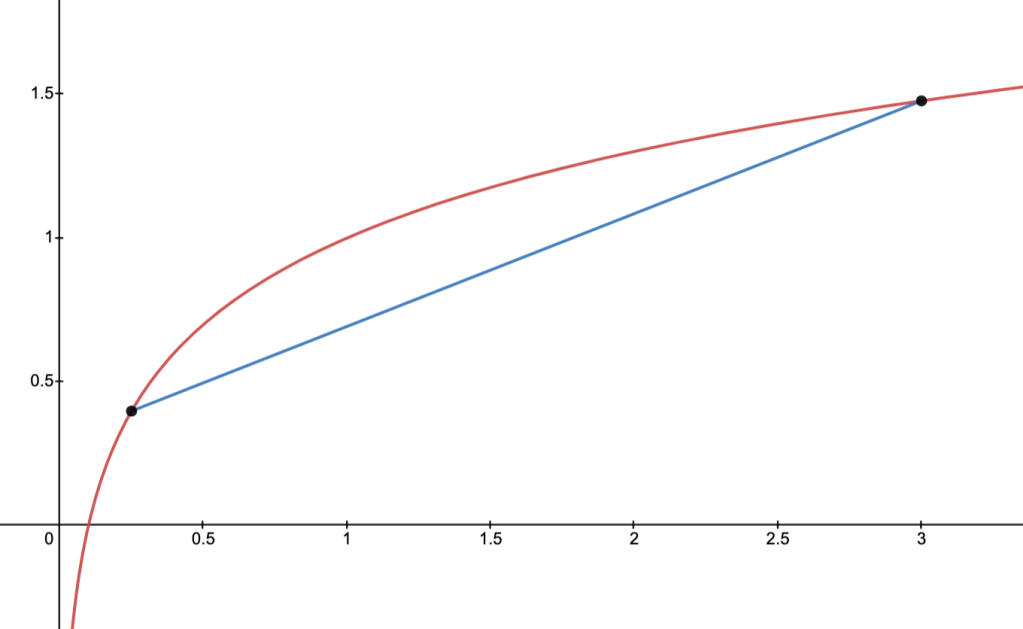
To give insight, consider the image below, where the thick line is the “graph” ofand the dashed line is the “secant line” connecting the points
to
for any
.

Examples
- All linear functions are convex and concave on their domains.
-
is convex on
.
-
is convex on
for
.
-
is convex on
for
or
and concave for
.
-
is convex on
- If
is convex, then its indicator function
is convex (in the extended value sense).
One Dimensional Characterization
Proposition. Let
and
,
.
Proof.
Step 1.
First note thatStep 2. ( )
)
Suppose Then, for
Step 3. ( )
)
Suppose now that each Fix
We want to show
.
,
Since
First Order Characterization
Proposition. If
.
Proof (sketch).
We prove it in caseThroughout, let
Step 1. ( )
)
If
Step 2. ( )
)
Supposing
Remarks.
-
For fixed
, the mapping
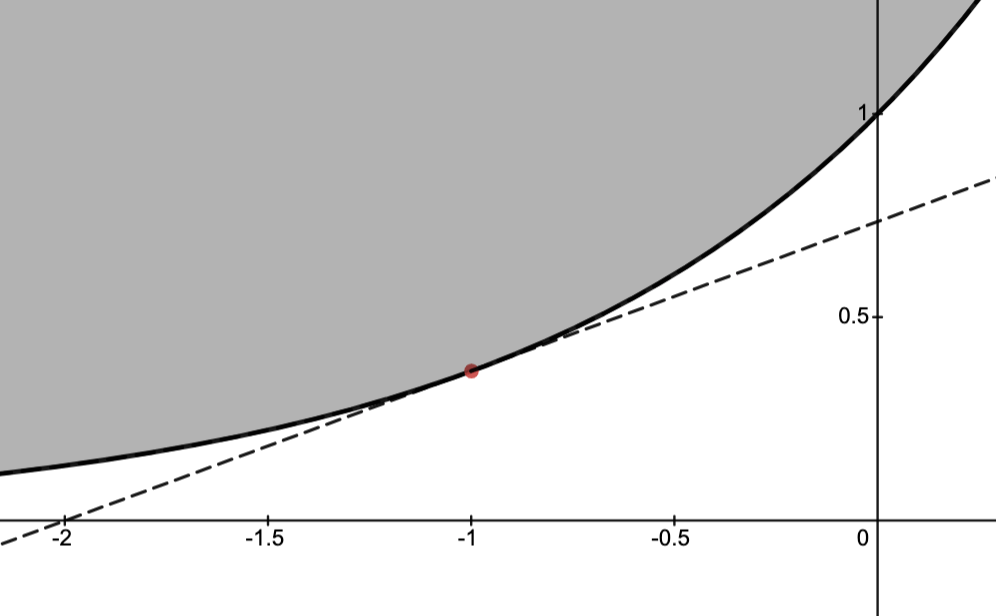
is affine whose graph is a hyperplane passing through the point.
Therefore, the inequalitymeans this hyperplane is a tangent plane at
of the graph of
lying under the graph of
.
In fact, this plane is a supporting hyperplane of the epigraph
at the point.
-
The affine mapping
is just the first order Taylor approximation of
at
.
Thus, differential convex functions are such that their first order Taylor approximations serve as a global underestimators of.
Second Order Characterization
Proposition. If
.
Recall: if
Proof (sketch).
Step 0.
The proof is a little more involved, so let us just give two intuitive justifications.Justification 1.
The second order Taylor approximation gives
The first order approximation from Convex Function Theory.First Order Characterization then implies convexity.
Justification 2.
Another intuitive justification is thatRemarks.
-
Recall: for
, there holds
-
for all
implies
is strictly convex.
Converse is false sinceis strictly convex.
Level Sets
Fix a function -Sublevel set:
-Sublevel set:
the set
Each shade of gray indicates a new sublevel set and of course
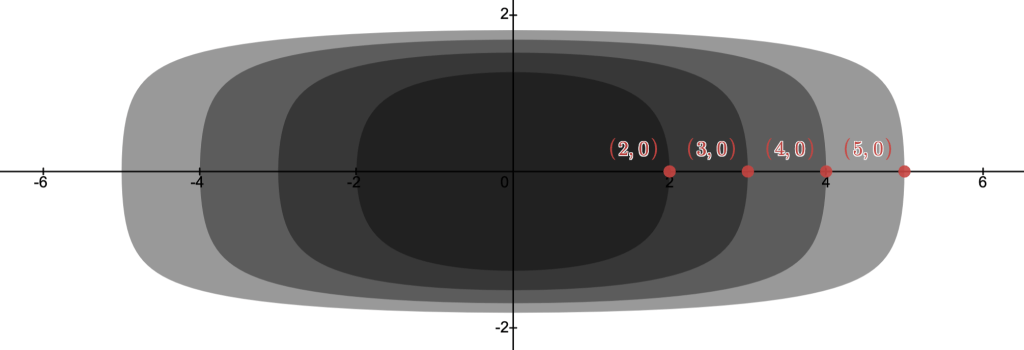
 -Superlevel set:
-Superlevel set:
the set
.
Each shade of gray indicates a new superlevel set and of course
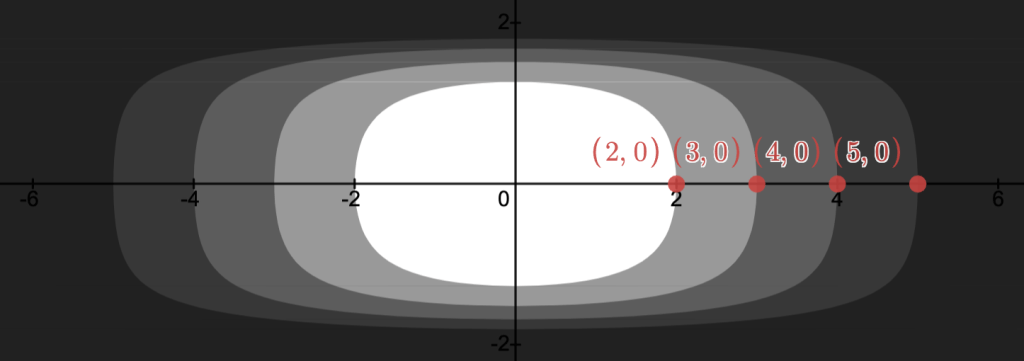
Proposition. If
Equivalently, if
Proof.
Want to show:If
and hence
Graphs
Fix a functionProposition.
Equivalently,
Proof. (sketch)
We consider the caseStep 1. ( )
)
Suppose If
Let
(If at most one intersection point exists, then it is easy to see that the line connecting
By convexity of
This shows
Step 2. ( )
)
Suppose now Let
Then
But convexity of
This is enough to conclude
Convex Calculus
The following list details some operations and actions that preserves convexity.The main point: to conclude a function
N.B.: Conclusions only holds on common domains of the functions.
Conical combinations:
convex and
convex.
Weighted averages:
convex in
,
convex.
Affine change of variables:
convex,
,
convex.
Maximum:
convex
convex.
Supremum:
convex in
for each
convex.
Justification.
For
Example.
Let
Thus
Infimum:
convex in
convex
finite for some
convex on
.
Fenchel conjugation
LetFenchel conjugate:
N.B.:
;
Intuition.
SupposeFor a given unit price
.
N.B.:
Thus,
Viz.: the
The tangent line through
Lastly, note that the
Remarks
-
Often
is just called the conjugate function of
.
-
Since
is the supremum of a family of affine functions,
is always convex, even if
is not.
(Follows from Convex Function Theory.Convex Calculus. - If
-
is convex
-
is a closed subset of
,
.
-
Example.
We will compute the conjugate function of
Thus, let
Case  :
:
as
.
.
Case  :
:
Compute
Case  :
:
Compute
,
Conclusion:
Since
for
,
Legendre Transform
LetThen, the Fenchel conjugate
Proposition. If
.
Proof.
Step 1.
Let
.
maximizes
iff
Step 2.
Using Step 1. and
iff
maximizes
.
Step 3.
Letting
,
Example 1.
Let
,
.
; i.e.,
.
,
Example 2.
Fix
.
Step 0.
Observe-
is convex:
(Justification)
Consider case.
Let.
Thus.
Easy now to see.
implies
is invertible since then
.
Step 1.
Using
Step 2.
LetBy preceding proposition and Step 1., there holds
Other Notions of Convexity
There are two other important notions of convexity that we will return to if needed.Let
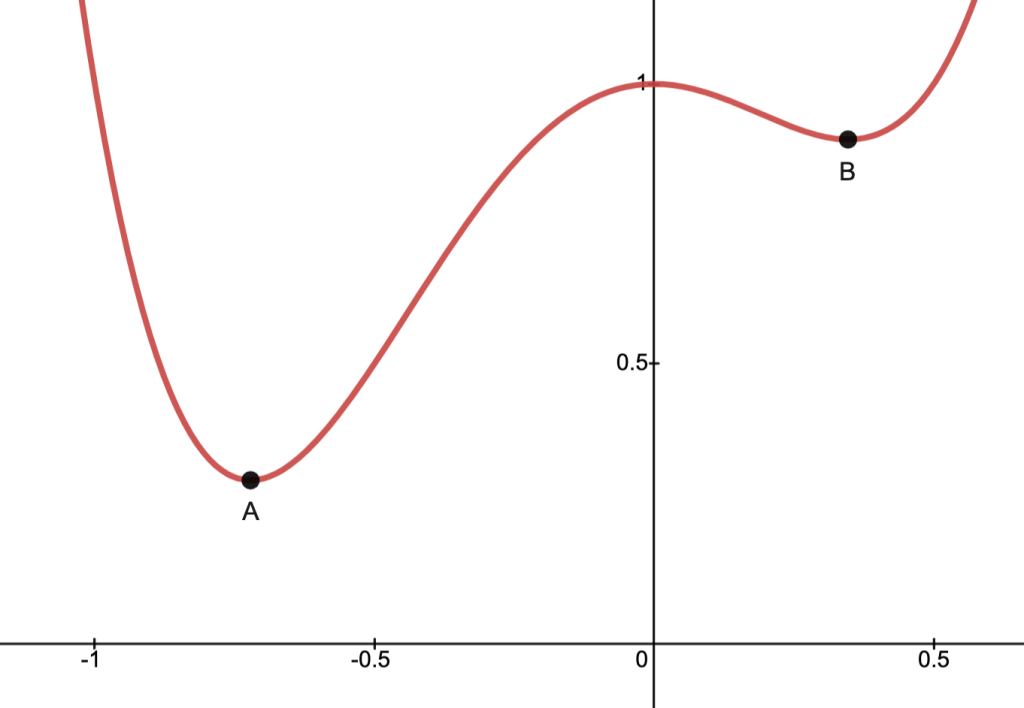
Quasiconvexity:
Features:
- Quasiconvex problems may sometimes be suitably approximated by convex problems.
- Local minima need not be global minima
Log-convexity:
for all
.
Generalized Convexity
Let
.
.
Examples
-
(CO Example 3.47)
Let.
Thenis
-convex iff:
is convex and for all
and
, there holds
which holds iff
for each, i.e., iff
is component-wisely convex.
-
(CO Example 3.48)
A functionis
-convex iff :
is convex and for all
and
, there holds
N.B.:.
-
this is a matrix inequality and
-convexity is often called matrix convexity.
-
is matrix convex iff
is convex for all
.
-
The two functions
are matrix convex.
-
this is a matrix inequality and
Basics of Optimization Problems
General Optimization Problems
By an optimization problem (OP) we mean the following:
the objective function;
the optimization variable or parameters;
,
, the inequality constraint functions; and
,
, the equality constraint functions.
.
Feasibility
Consider an (OP) as above.Feasible point: those
Feasible problem: A problem with nonempty feasible set, i.e.,
Infeasible problem: A problem with empty feasible set; i.e., there are no
Remark.
-
A feasible problem need not have a solution; e.g.,
has no minimizer nor minimum on
.
- An infeasible problem never has a solution–there are no parameters
to even test.
Basic Example
Consider the problem
The objective function is
,
The inequality constraint functions are
.
The domain of the problem is
.
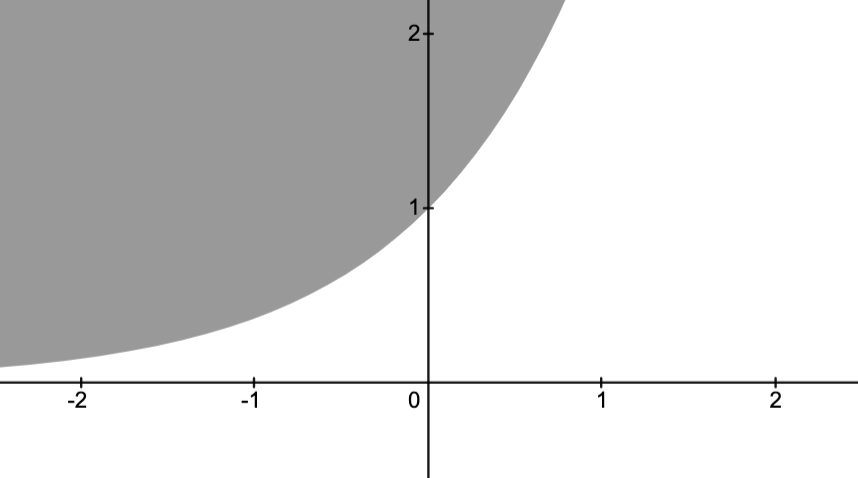
The feasible set:
Let
.
Note that the darkest region given by

Can we solve the problem?
Noting-
as
approaches a point on the circle
, and
- such sequences exist in the feasible set,
The Feasibility Problem
Feasibility problem: Given an (OP) with
Example 1.
The problem
This is depicted below.
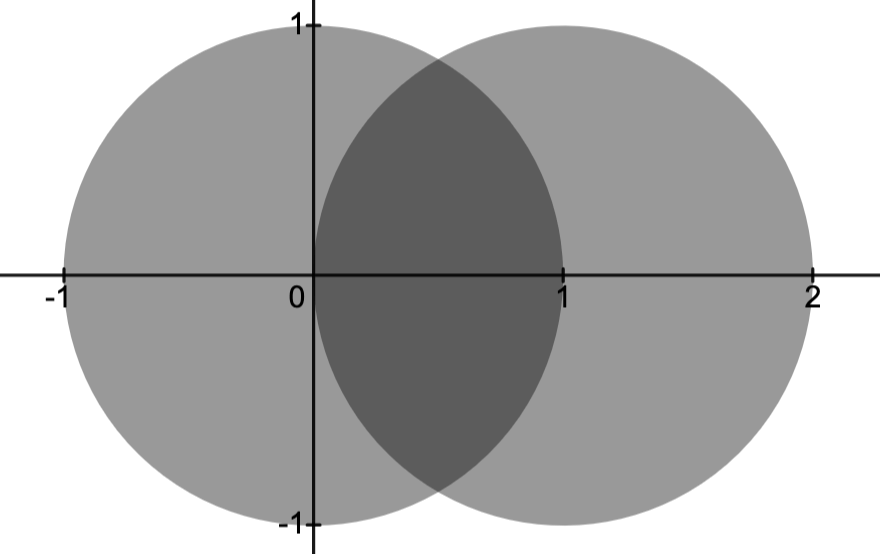
Optimal Value and Solvability
Recall:
Optimal value:
The value
,
N.B.:
Solvable:
When the problem satisfies
there exists with
,
Remarks.
-
iff the (OP) is solvable.
Indeed,is not well-defined unless the (OP) is solvable.
-
need not be finite:
if
is unbounded below on the feasible set; and
if the OP is infeasible.
Standard Form
Optimization problems need not be placed in the form we defined them.We therefore introduce the following definition.
(OP) in Standard form:
Example: Rewriting in standard form.
We can recast more general optimization problems in standard form; e.g., consider
(noting
)
for
for
Equivalent Problems
Suppose we are given two OP’s: (OP1) and (OP2).We say (OP1) and (OP2) are equivalent if: solving (OP1) allows one to solve (OP2), and vice versa.
N.B.: Two problems being equivalent does not mean the problems are the same nor that they have the same solutions.
Example.
Consider the two problems:
minimizes
on
minimizes
on
,
Indeed, if we find the solution
Change of Variables
SupposeThen, under the change of variable
Moreover, injectivity may be dropped.
Justification.
Indeed,-
if
solves (OP1), then
solves (OP2).
(More generally,such that
solves (OP2).)
-
if
solves (OP2), then
solves (OP1).
Example
Consider the problem
.
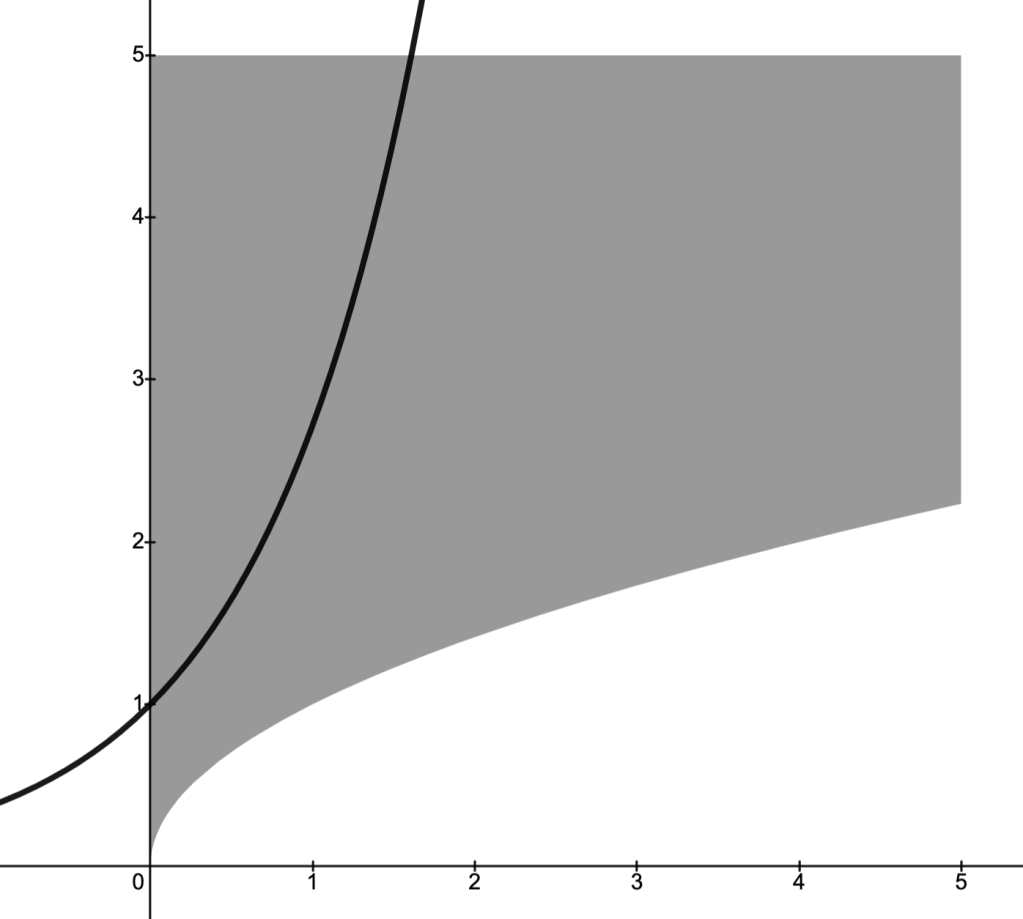
.

Eliminating Linear Constraints
LetLet
Then
Consequently
Justification.
Indeed,- if
solves (OP1), then any
with
solves (OP2), and
- if
solves (OP2), then
solves (OP1)
Example.
Consider the minimization problem
But, to match with above: let
.
.
Therefore, the minimization problem becomes
Thus, the original problem has solution
.
Slack Variables
GivenUsing slack variables
Remarks.
-
All of the
which may satisfy the constraints of (OP2) are the same as those which satisfy the constraints of (OP1); this justifies the equivalence.
-
Let
be the feasible set of (OP1) and
that of (OP2).
Thenand
; i.e., the feasible sets are not the same object.
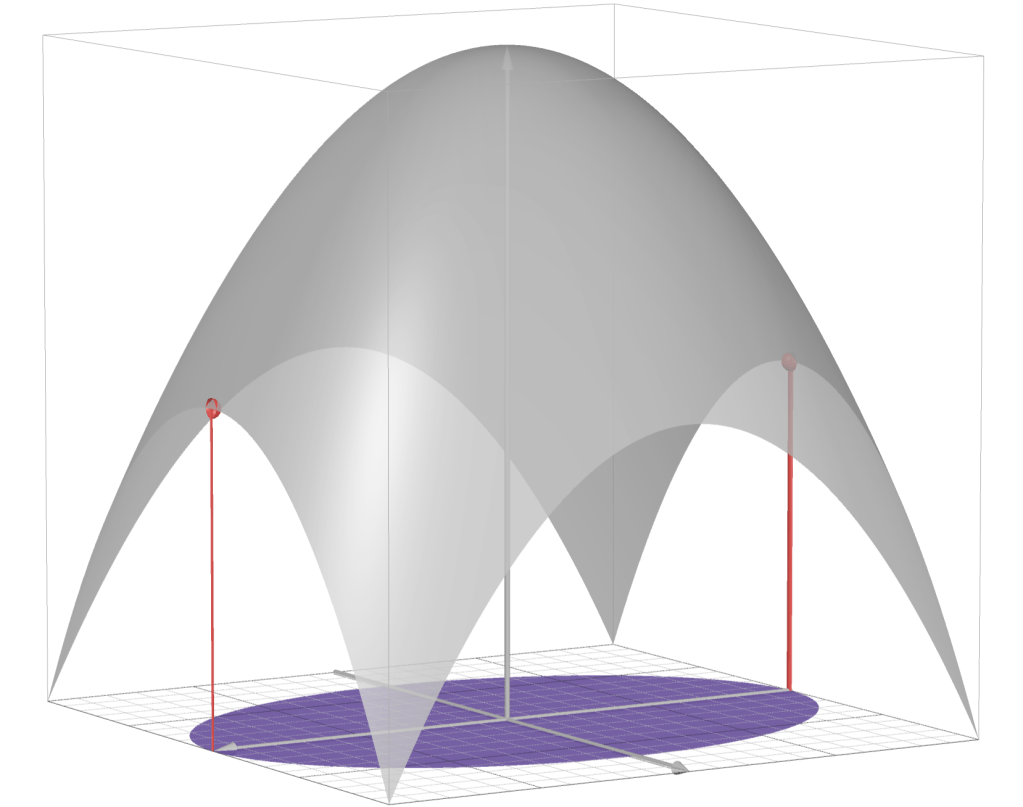
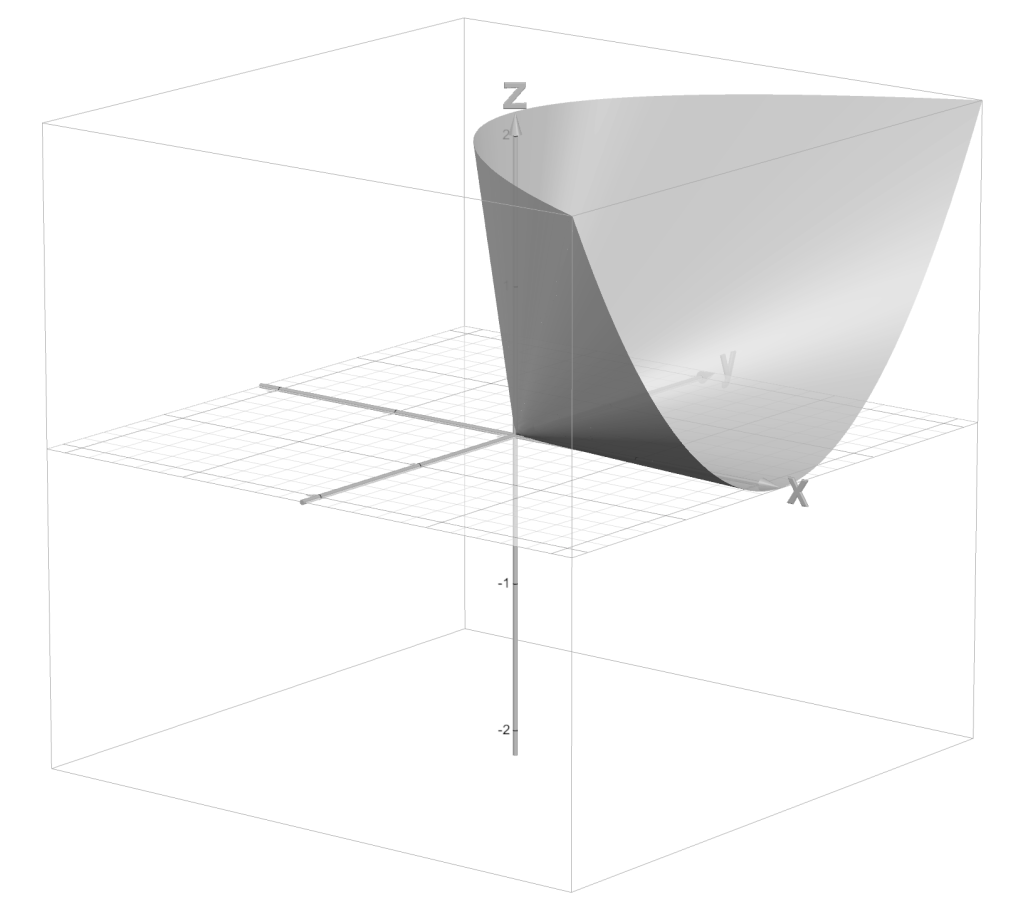
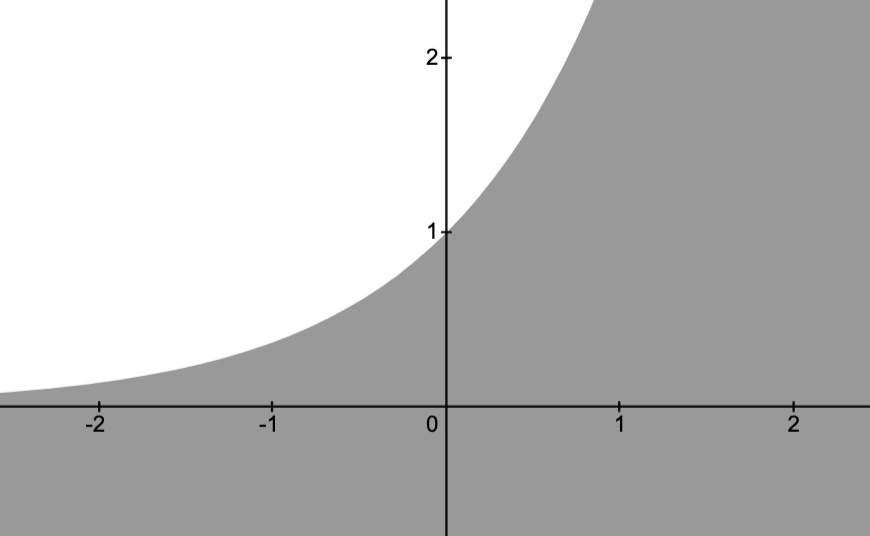
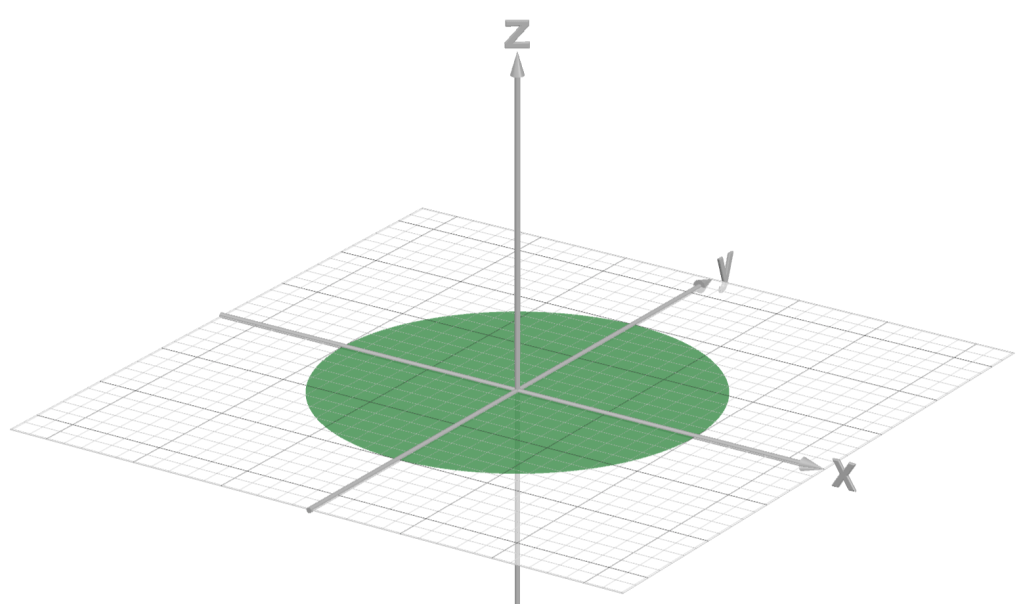
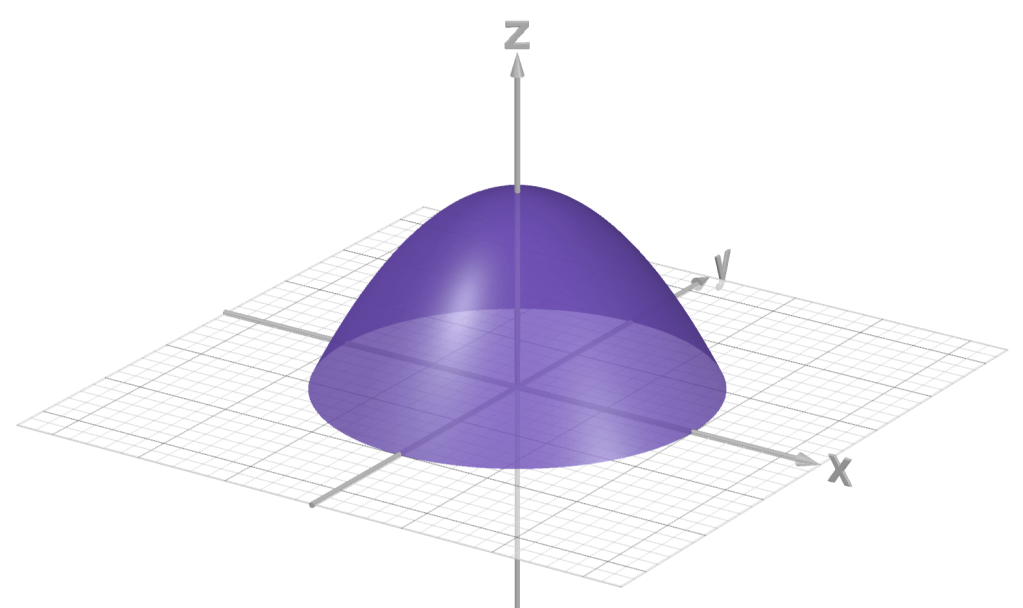
- Example: in the images below, the disk depicts a feasible set
and the paraboloid-type set depicts the feasible set
with slack variable
.
N.B.: the permissiblecoordinates are the same for both sets.
Main point:
Solving the system of equations
Example.
Consider
.
Moreover, one can solve the problem
Epigraph Form
Recall:The optimization problem
Fragmenting a Problem
Proposition. Given
.
Viz., to minimize a function on a set
Example.
Consider the (OP)
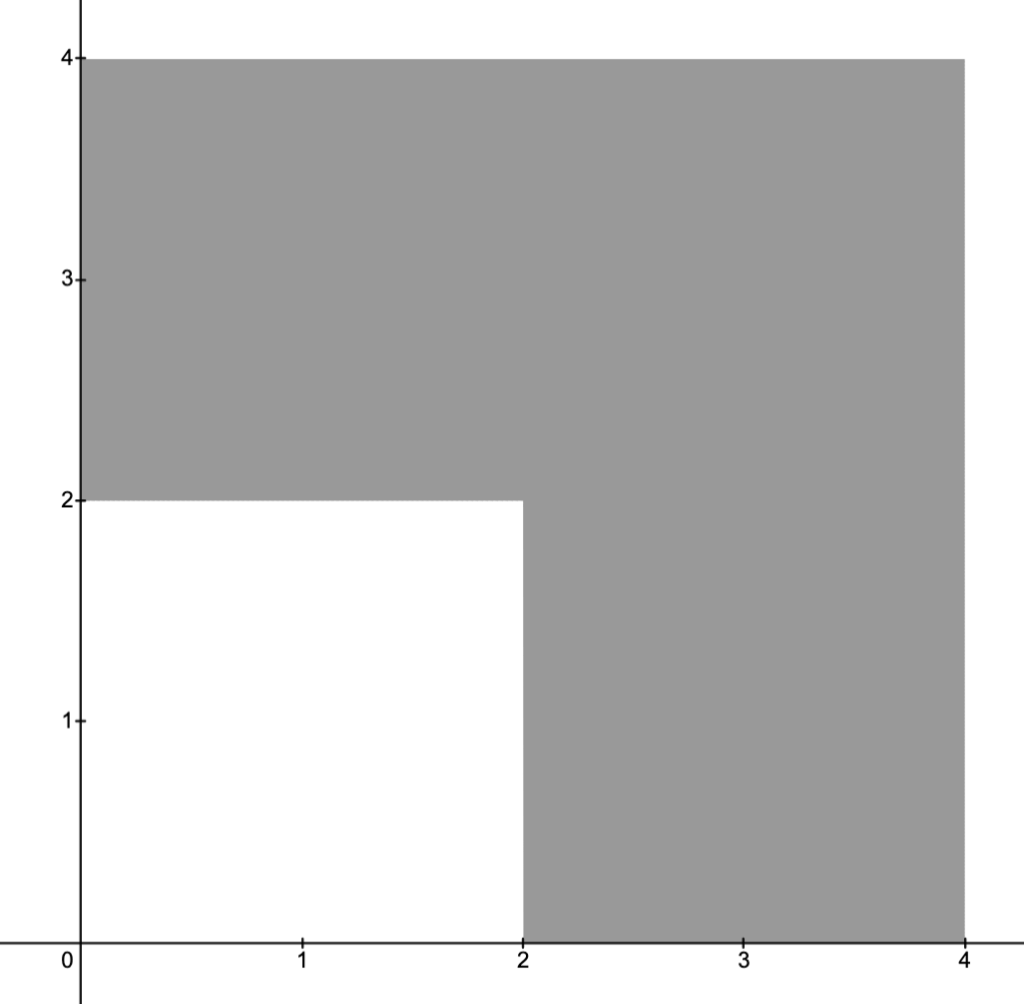
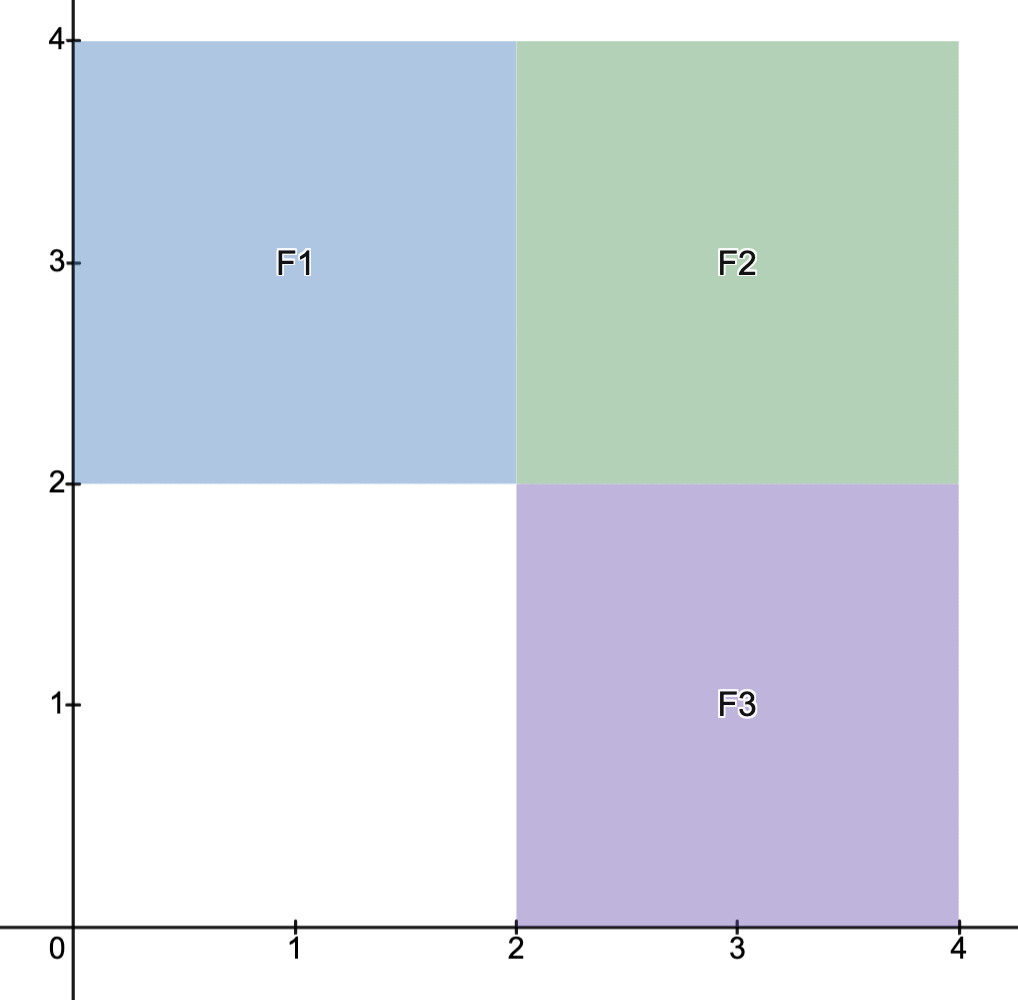
Using the preceding proposition, the optimal value of (OP) is given by
.
Basics of Convex Optimization
Convex Optimization Problems
Abstract convex optimization problem: A problem involving minimizing a convex objective function on a convex set.Convex optimization problem: a problem of the form
-
and
are convex; and
-
and
are fixed.
Some Remarks
Remark 1.
As defined, a (COP) is an (OP) in standard form; naturally, there are nonstandard form (OP)’s equivalent to (COP)’s.E.g., the abstract (COP)
.
Remark 2.
We emphasize: the equality constraints are assumed to be affine constraints.Moreover, the equality constraints
,
.
Remark 3.
The affine assumption on the equality constraints can be lifted at the possible expense of an intractable theory/numerical analysis.E.g., if
Remark 4.
Generally,Remark 5.
The common domain
Optimality for Convex Optimization Problems
Assume throughout thatProposition 1. If
Proof.
We will follow a proof by contradiction; i.e., we will show that assumingStep 1.
Step 2.
SupposingBy choice of
Step 3.
Set
It follows that
Step 4.
Since
.
.
Proof.
Step 0.
N.B.: since
.
Step 1.( )
)
Suppose
Set
Using
,
Since
Additional justification
SinceStep 2.( )
)
Supposing
.
Proof.
By Proposition 2., we have that
Differentiability of
.
Some Examples
Example 1.
Let
.
C.f.,Convex Function Theory.Second Order Characterization. By the preceding corollary, we have
.
Three cases:
is unbounded below and hence (OP) is unsolvable;
is invertible and so
is the unique solution to (OP);
and
has an affine set of solutions.
Example 2.
Let
.
Two cases
is an inconsistent system
the problem is infeasible.
is a consistent system; then
,
for some
.
In case 2., we have
and
.
for all
,
.
.
Linear Programming
Linear program: a (COP) of the form
,
Recall ( ):
):
For
.
Different than:
Determining the Feasible set:
Step 1. ( )
)
Given
Step 2.
Given
Step 3. ( )
)
Given
Step 4.
Steps 1. and 3. imply the feasible(c.f. Convex Geometry.Polyhedra.)
Example.
Let

Remarks.
-
Given
, have equivalent problem with objective
.
Indeed,
WLOG: can assumeto solve problem.
-
Since
one also calls the problem of maximizingover a polyhedron a (LP).
Example: Integer Linear Programming Relaxation.
Integer Linear Program: an (OP) of the form
N.B.: An (ILP) is not a convex problem, but may be approximated by one (see below).
The feasible set
Let
Then
.
Example. Consider an (ILP) with constraints given by
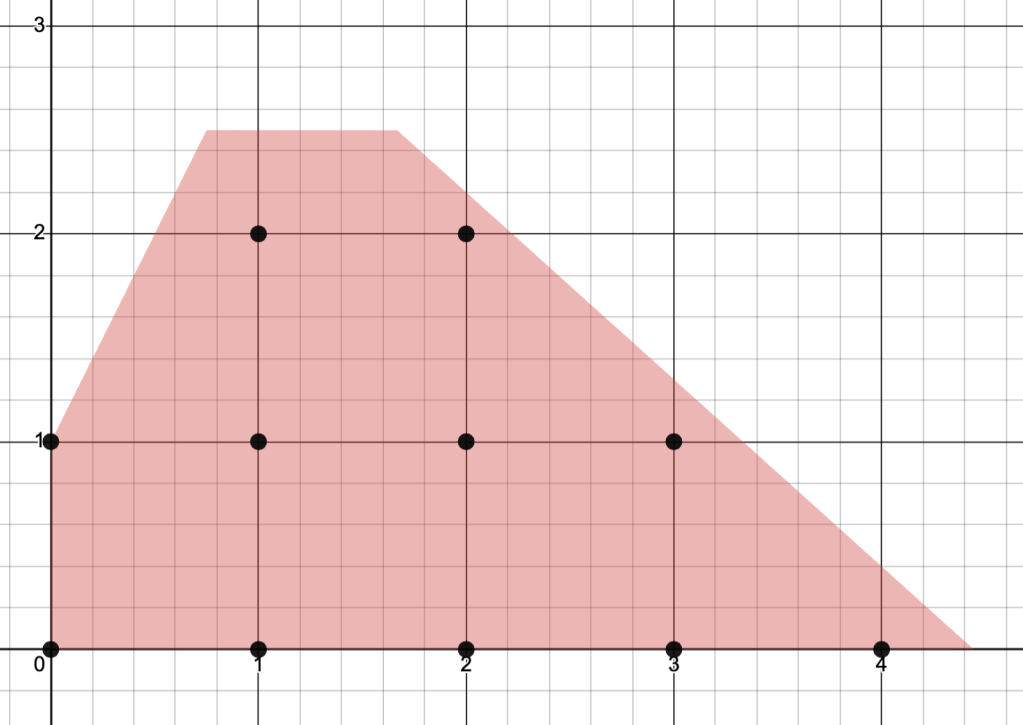
Remarks.
-
Can of course also impose equality constraints
:
-
If we impose
, then the problem is called a boolean linear program:
Suitable for when coordinates ofindicate when something is “off” or “on” or decision is “no” or “yes”.
Can also useinstead.
Relaxation of (ILP)
The LP
Important points:
-
The “tightest” convex relaxation is given by
Generally speaking, finding the convex hull is not an efficient way of approaching (ILPs). - The relaxation (LP) of (ILP) is generally easier to solve, though exact algorithms exist for (ILP).
-
If
then.
(Indeed the relaxation has larger feasible set.) -
If
solves the (LP), then it solves the (ILP).
Relaxation of (BLP)
Explicitly, a (BLP) is of the form
N.B.: the relaxation
.
Example.
Problem Given- assign each worker to work at some location
- assign at most one worker to a location
- minimize cost of operation and transportation
Construct objective function
We find
Construct constraints
The constraint that
Since each worker is selected only once, we have
.
Formulate Problem
Putting everything together, the (BLP) formulation of the problem is
Quadratic Programming
Quadratic program: an (OP) of the form
Remarks.
-
As for (LP), the constraints
describe a polyhedron.
-
Given
, then
WLOG: can assumeto solve problem.
-
If
then,
Thusimplies
is convex.
N.B.: The factoris just a convenient normalization.
-
The generalization
results in quadratically constrained quadratic programming (QCQP).
Imposingensures the (QCQP) is convex.
(C.f., Convex Function Theory.Level Sets.)
-
The generalization
also results in a (QCQP), but this can break convexity.
E.g., The quadratic constraints
result in a (BLP) since these constraints enforceor
, respectively.
-
There holds
-
The assumption
(i.e.,
) is not a serious restriction.
Indeed, first note that, sinceis a scalar, we have
.
Let.
Thus,
where.
Lastly, observe the symmetry of:
.
Thus every quadratic
has a “symmetric representation” of the formwith
.
Example: Least Squares
Least squares: an unconstrained (QP) of the form
Features:
-
WLOG: may assume columns of
are linearly independent, and so
.
-
N.B.: a least norm solution to (LS) is generally given by
where,
is the pseudo-inverse (aka Moore-Penrose inverse) of
.
-
Under the WLOG assumption, there holds
.
Recall (definition of  )
)
For
.
Rough Justification of WLOG
Let
Therefore, we may write
.
Computing
.
Therefore, a (LS) problem with matrix of size
This argument holds in general: if
Remarks.
-
If
has solution
, then
solves the (LS) problem.
-
If
has no solution, then any
solving the (LS) problem gives a “best” estimate solution to
, where “best” is chosen to mean in terms of the vector norm
.
-
While minimizing
is equivalent to minimizing
, the exponent
ensures
is differentiable (at
).
(C.f.:is not differentiable at
, but
is.)
Solving the (LS)
Step 1. (The problem is convex)
The objective function
.
-
and so
, i.e.,
is symmetric;
-
for all
there holds
i.e.,,
.
Step 2. (The critical points)
We compute
.
Step 3. (The solution)
By corollary proved above:Moreover,
- linear independent columns
iff
.
.
- Since
is square, can conclude
is invertible.
Lastly: since
iff
.
Example: Distance Between Convex Sets
LetNearest Point Problem (NPP): Among
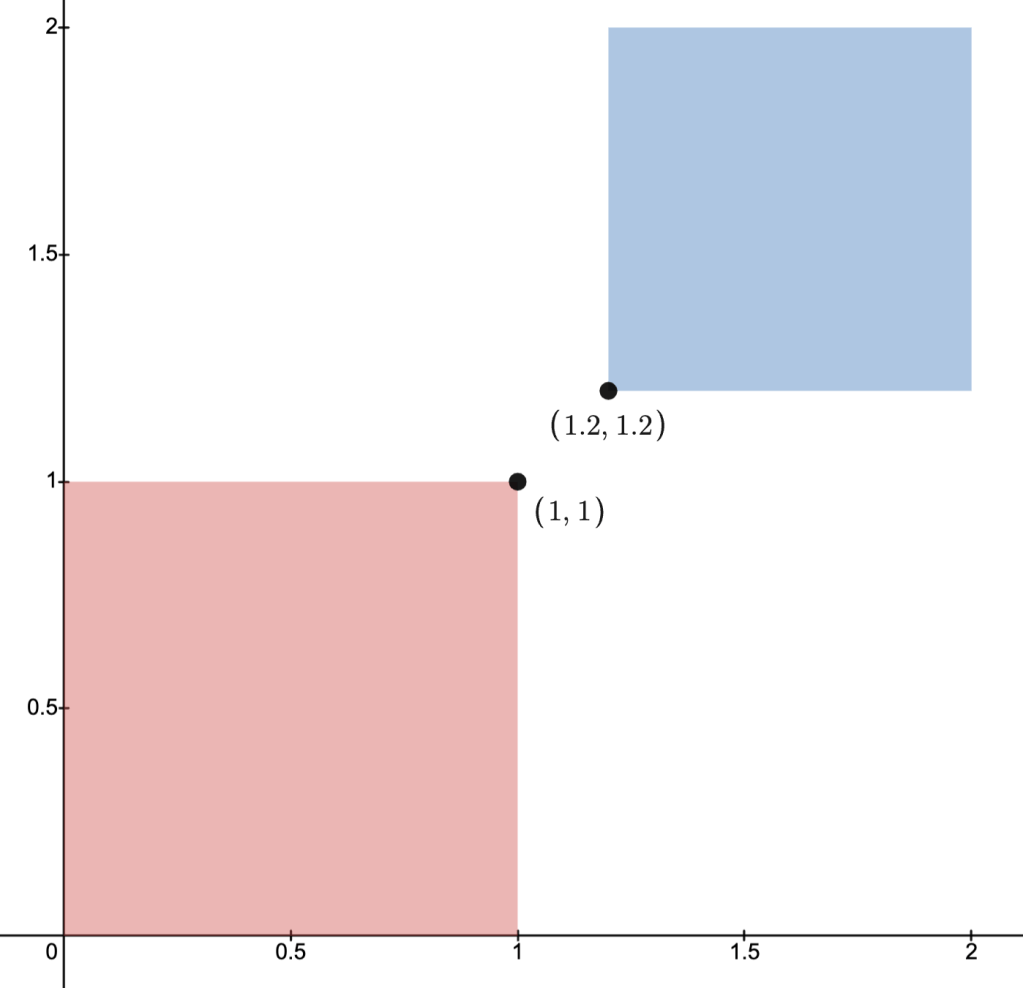
The (NPP) may be expressed as a standard form (COP).
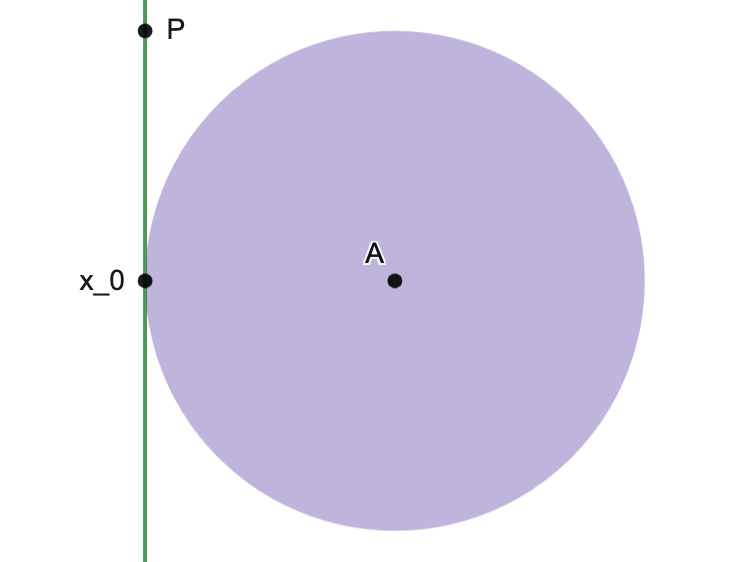
Indeed, supposing
When the
Indeed, supposing
Polyhedral Approximation.
Let
Geometric Programming
Monomial function: given
,
.
,
Remarks.
-
Let
Since any monomial is a posynomial, we have.
-
If
then
Thusis a group and
a “conic representation” of
.
-
As usual, we use the language “writing in standard form” to refer to writing an equivalent (OP) written in the form (GP) above.
General (OPs) clearly equivalent to a (GP) may be called a geometric program in nonstandard form.
For example, the geometric program
with
is readily rewritten as a standard form (GP):
Rewriting (GP) as a (COP)
General (GPs) are not convex (e.g.,However, any (GP) is easily recast as a (COP) via change of variable.
Step 1. (The change of variable)
We will write
Step 2. (Monomials  convex function)
convex function)
Let
convex
convex
Step 3. (Posynomial  convex function)
convex function)
For
Step 4. ((GP)  (COP))
(COP))
We explicitly write the (GP) as:
Step 5. ((GP) in convex form)
At last, since exponentiation may result in unreasonably large numbers, it is customary to take logarithms, resulting in the geometric problem in convex form:
-
Concavity of
is too weak to break the convexity of
, and so the problem is still convex.
-
The constraints are equivalent since
is monotonic and injective on
.
Example.
(Taken from Boyd-Kim-Vandenberghe-Hassibi: A tutorial on geometric programming)Problem Maximize the volume of a box with
- a limit on total wall area;
- a limit on total floor area; and
-
upper and lower bounds on the aspect ratios
and
.
The volume of the box is
.
Construct contraints
Putting everything together, we realize the problem may be formulated as the following (GP):
Semidefinite Programming
(Heavily influenced by Vandenberghe-Boyd Semidefinite Programming.)Linear matrix inequality (LMI): given
.
Semidefinite program (SDP): an (OP) of the form
Convexity of Feasible Set.
To see that (SDP) is a convex problem, first note: if and
.
.
Example 1. LPs are SDPs
Consider the (LP)
Given
Since
.
Letting
,
.
Therefore, using
Therefore, defining
.
In conclusion, we have that the (LP)
Example 2. Nonlinear OP as a SDP
Consider the nonlinear (COP)
N.B.:
-
choice of domain (a halfspace) of objective and ensures convexity.
-
concave problem.
.
.
.
Indeed, evidently,
and
.
.
To make it clearer, introduce the notation
Lagrangian Duality
Throughout, let (OP) denote a given optimization problem of the form
Recall:
The Lagrange Dual
Lagrangian: the function
.
Lagrange multipliers: the variables
The vectors
Lagrange dual function: the function
.
N.B.: as an infimum of affine functions,
Proposition. For
,
,
Proof.
-
Let
be feasible.
Then
-
Let
and
be arbitrary.
Then feasibility ofimplies
Consequently,
-
Therefore, for all feasible
, for
and for arbitrary
, there holds
and so
(Indeed,.
is a lower bound of
and
is the greatest lower bound of
.)
Lagrangian as underestimator.
(See CO 5.1.4)
Define the indicator functions
N.B.: if
.
In particular, for each
Example 1
Consider the least squares problem
.
.
Therefore, the Lagrangian
N.B.:
Consequently,
,
In conclusion,
Example 2
Consider the linear program
.
-
equality constraints given by
.
-
iff
iff.
Therefore, the Lagrangian for (LP) is
Want to compute
Therefore,
.
Therefore, the Lagrange dual is
In particular, for dual feasible
Return of Conjugate Function
Recall: given
Consider the the (OP)
The Lagrangian is
We may now compute the Lagrange dual in terms of the conjugate
,
Appendix
Differentiating 
Given
,
.
Differentiating 
Given
.
.
Example.
Let
Differentiating 
Given Using the Taylor expansion
.